[논문 리뷰] Denoising Diffusion Probabilistic Models 이해하기

지난 VAE 포스팅에 이어서 이번 포스팅에서는 Denoising Diffusion Probabilistic Models, 흔히 DDPM으로 널리 알려진 diffusion 모델에 대해서 설명하려고 합니다. 큰 흐름은 논문을 따라가고 있지만, 일부분은 제가 이해하기 쉬운 순서대로 재배치했습니다.

DDPM과 VAE

VAE와 DDPM 모두 학습 데이터 $X$를 기반으로 latent를 추출하고, 이를 바탕으로 데이터를 재구성해나간다는 점에서 유사한 구조를 가지고 있습니다. 아마 이 두 모델의 큰 차이점은 latent를 얻는 데에 한 step만을 필요로 하는지(VAE), 또는 여러 step을 거쳐 점진적으로 만들어 나가는지(DDPM) 일겁니다. $X$를 입력으로 받아 직접적으로 $\mu$와 $\Sigma$를 출력하여 latent의 분포를 예측하는 VAE와 다르게, DDPM은 $X$에 점진적으로 noise를 입히는 과정을 통해서 latent를 만들어냅니다. 그 과정이 어떻게 이루어지는지 아래 그림을 보면서 다시 설명드리겠습니다.

DDPM은 입력 이미지 $x_{0}$로 부터 시작해서 우선 noise를 입혀나가는 과정인 forward process를 거치게 됩니다. 이 때 총 $T$번의 스텝을 통해 noise가 충분히 입혀지게 되고, $x_{T}$는 Gaussian noise가 됩니다. 우리는 Gaussian noise, 즉 $x_{T}$로 부터 noise를 걷어내는 reverse process를 학습시키는 것이 목표입니다.

Forward Process

Forward process는 $t-1$번째 step의 이미지 $x_{t-1}$에 Gaussian noise를 더하여 $x_{t}$를 만들어가는 과정입니다. 이 때 각 단계에서의 process는 바로 이전 단계의 상태에만 영향을 받는 Markov Chain이 되도록 설계합니다. Forward process $q(x_{t}|x_{t-1})$는 아래와 같이 나타낼 수 있습니다.

우리는 reparameterization trick을 활용해 $x_{t}=\sqrt{1-\beta_{t}}x_{t-1}+\sqrt{\beta_{t}}\cdot \epsilon_{t-1}, \epsilon\in\mathcal{N}(0,I)$로 나타낼 수 있습니다. VAE와 마찬가지로, 이런 식으로 sampling이라는 미분 불가능한 연산을 우회해서 DDPM의 loss를 계산할 때 활용할 수 있는 형태로 $x_{t}$를 바꿔줄 수 있습니다.

$\beta_{t}$는 주입되는 noise의 크기라고 생각하시면 됩니다. $\beta_{t}$의 경우 reparameterization을 활용하여 학습을 통해서 얻을 수도 있지만, DDPM 저자들은 fixed constant를 써도 상관없다고 합니다. DDPM에서는 실제로 $\beta_{t}$를 hyperparameter로 미리 지정해주기 때문에, forward process에서는 학습할 parameter가 없습니다. 저자들은 step을 거듭할수록 $\beta_{t}$가 점진적으로 커지도록 설정해줬습니다. 이 때, $\beta_{t}$가 실제 data scale보다 훨씬 작은 값을 가진다면, 우리는 $x_{t}$를 구하기 위해 $t$번의 noise 더하기를 하지 않고, 아래와 같은 식으로 한 번에 $x_{t}$를 구할 수 있음이 증명되어 있습니다.

여기서 $\alpha_{t}:=1-\beta_{t}$, $\bar{\alpha_{t}}:=\Pi_{s=1}^t\alpha_{s}$ 를 뜻합니다. 실제로 저자들은 데이터의 scale $[-1,1]$에 비해 훨씬 작은 $\beta_{t}$를 설정하여 ($\beta_{1}=10^{-4}$ to $\beta_{T}=0.02$) 위 식을 활용하였습니다.

Reverse Process

Forward Process에서 이미지에 noise를 씌워서 Gaussian noise로 만들었으니, 이제는 noise를 제거해나가며 원래 이미지로 복원할 차례입니다. Noise를 제거하는 과정 역시 Gaussian noise를 더해간다는 점에서 forward process와 유사하지만, 올바르게 noise를 제거하기 위해선 올바른 Gaussian noise를 더해줘야 할 것입니다. 우리는 이 올바른 Gaussian noise를 구하기 위해서 neural network $\theta$를 학습한다고 해도 무방합니다. 이 과정을 식으로 나타내면 다음과 같습니다.

즉, 우리는 network를 통해서 reverse process에 쓰일 Gaussian noise의 평균과 분산 값을 예측하는 것이 목표라 할 수 있습니다.

Training DDPM

DDPM 역시 많은 생성 모델들처럼 likelihood를 maximize하는, negative log likelihood(NLL)를 loss 함수로 활용하여 학습합니다. NLL은 직접 구하기 어렵기 때문에, VAE의 ELBO와 마찬가지로 NLL의 upper bound를 minimize하는 방식으로 학습을 진행합니다. NLL의 variational bound를 구한 후, 수식을 요리조리 변형시키다 보면 아래와 같은 결과를 얻을 수 있습니다.

수식을 유도하는 것은 몹시 복잡한 관계로 생략하겠습니다. 혹시 과정이 궁금하시다면 설명을 굉장히 잘해두신 블로그가 있으니 참고하시면 됩니다. 여기서는 upper bound 각각의 의미와 구하는 과정을 살펴보도록 하겠습니다. 여기서 $\mathbb{E_q}$는 1에서 $T$번째 사이의 $x_{t}$ 값의 분포가 $q$를 통해 얻어진 값을 따른다는 뜻입니다. 수식으로 표현하면 $x_{1:T}\sim q(x_{1:T}|x_{0})$ 정도가 되겠습니다.

먼저 $D_{\text{KL}}(q(x_T|x_0)||p(x_T))$, 논문에서는 $L_T$로 나타낸 이 항은 $p(x_T)$와 $q(x_T|x_0)$ 사이의 거리를 나타냅니다. 즉, latent $p_\theta(x_T)$가 $q(x_T|x_0)$에 가까워지도록 유지하는, VAE의 Regularization loss 항과 비슷한 역할을 합니다. 그러나 VAE의 $q_\phi(z|x)$와 다르게 $q(x_T|x_0)$를 구하는 데에는 network parameter가 필요하지 않습니다. $\beta_t$를 상수로 고정시켰기 때문이죠. 따라서 $L_T$ 항은 network 학습 시에 활용할 필요가 없습니다.

세 번째 항 $-\text{log}p_{\theta}(x_0|x_1)$부터 살펴 보겠습니다. $x_{1}$이 주어졌을 때 $x_{0}$의 likelihood를 나타내는 항인데, 우리는 $x_{1}$의 분포가 $x_{0}$를 조건부로 한 forward process를 통해 얻어졌다고 했습니다. 즉, 간단하게 말하면 $x_{0}$를 넣었을 때 나오는 출력 값이 원래의 값과 얼마나 가까운지 나타내는 값인 겁니다. 이쯤 되면 VAE의 reconstruction error가 생각나시지 않나요? 세 번째 항은 VAE의 reconstruction error와 같은 역할을 하고 있습니다. 논문을 보면 복잡한 수식으로 설명하고 있는데, 실제로는 $x_{1}$을 넣어서 나온 결과와 $x_{0}$ 사이의 Euclidean distance로 구현합니다. (Gaussian 분포의 MLE 계산과 Euclidean distance 사이의 상관관계)

여기까지 살펴본 loss 함수들은 VAE에서 등장했던 함수들과 굉장히 유사합니다. 그러나 앞서 말했듯 VAE와 DDPM의 가장 큰 차이는 점진적인 noising, denoising step의 존재 유무입니다. 따라서, DDPM에서는 VAE에서는 존재하지 않았던 denoising process에 대한 loss 함수도 존재하게 됩니다. 지금부터는 denoising process 해당하는 loss 함수를 살펴볼 것입니다.

Denoising Process

Reconstruction loss와 Regularization loss를 제외하면 가운데 항이 남습니다. Sigma 내부의 항 $L_{t-1}=D_{\text{KL}}(q(x_{t-1}|x_t,x_0)||p_{\theta}(x_{t-1}|x_{t}))$의 의미는 꽤나 직관적입니다. Reverse process $p_{\theta}$에서 $x_{t}$에서 noise를 걷어내고 만든 $x_{t-1}$의 분포가 forward process에서 $x_{0}$, $x_{t}$가 주어졌을 때 $x_{t-1}$의 분포와 얼마나 가까운지를 측정하는 식이 됩니다. 더 쉽게 말하자면, reverse process가 얼마나 forward process의 역과정을 잘 모방했는지를 측정하는 겁니다. Noise을 입힌 과정의 반대로 denoising을 잘한다면 그만큼 원래 이미지를 잘 복원한다는 뜻일테니, 이 loss 항은 직관적으로도 잘 와닿습니다.

$q(x_{t-1}|x_{t})$의 경우 tractable하지 않지만, $x_{0}$가 condition으로 주어진 경우 아래와 같이 tractable 해집니다. (DDPM 논문 참고)

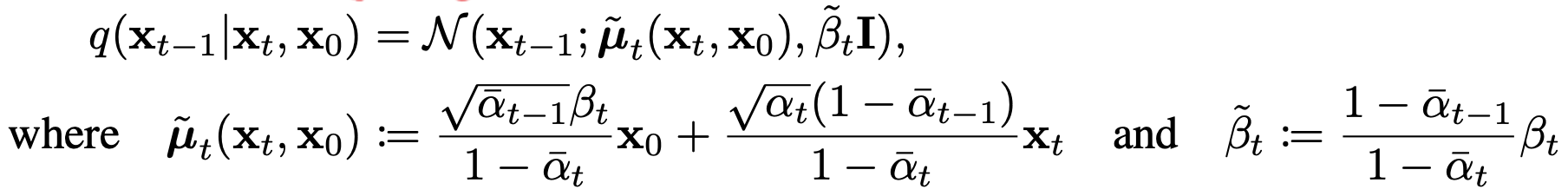
따라서, 우리가 KL-divergence를 구하고 싶은 분포들은 모두 Gaussian 분포라 할 수 있게 되었습니다. 두 Gaussian $\mathcal{N}(\mu_1,\sigma_1)$과 $\mathcal{N}(\mu_2,\sigma_2)$ 사이의 KL-divergence는 아래와 같이 나타낼 수 있으므로, 우리는 각 분포의 mean과 variance만 구하면 됩니다.

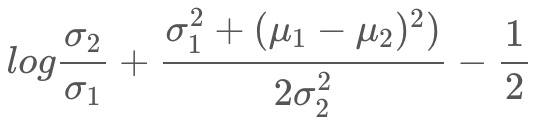
먼저, 저자들은 분산 $\Sigma_{\theta}(x_t,t)=\sigma_{t}^2\cdot I$로, $t$에 따라 변하는 상수로 설정합니다. 논문에는 $\sigma_{t}^2=\beta_t$ 및 여러 가지 시나리오에서 비교하는데, 여기에서는 학습 가능한 parameter가 아닌 상수로 설정했다는 점만 짚고 넘어가겠습니다. 따라서 우리는 위의 두 Gaussian 사이의 KL-divergence 식에서 network의 parameter에 영향을 받지 않는 항들을 묶어서 $C$로 표현하여 $L_{t-1}$을 아래와 같이 나타낼 수 있습니다.

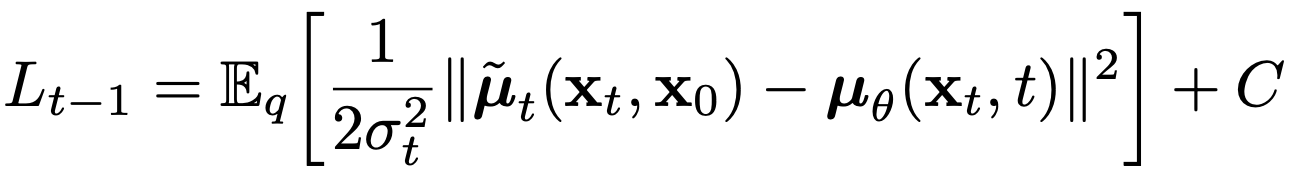
$L_{t-1}$이 조금 더 직관적인 메시지를 표현하게 되었군요. 우리가 학습하는 network의 목표는 $\mu_{\theta}$를 통해 $\tilde{\mu_t}$를 예측하는 것입니다. 이제 여기서는 loss를 더 단순화할 방법이 없을까요? 이 쯤에서 아까 구했던 식 $q(x_{t}|x_{0})=\mathcal{N}(x_{t};\sqrt{\bar{\alpha_{t}}}x_{0}, (1-\bar{\alpha_t})\cdot\text{I})$를 떠올려 봅시다. 우리는 reparameterization을 통해 $x_{t}$를 $x_{0}$와 $\epsilon$으로 이루어진 함수로 표현할 수 있습니다.

이를 활용하여 $L_{t-1}$을 다시 나타내면 아래와 같습니다.

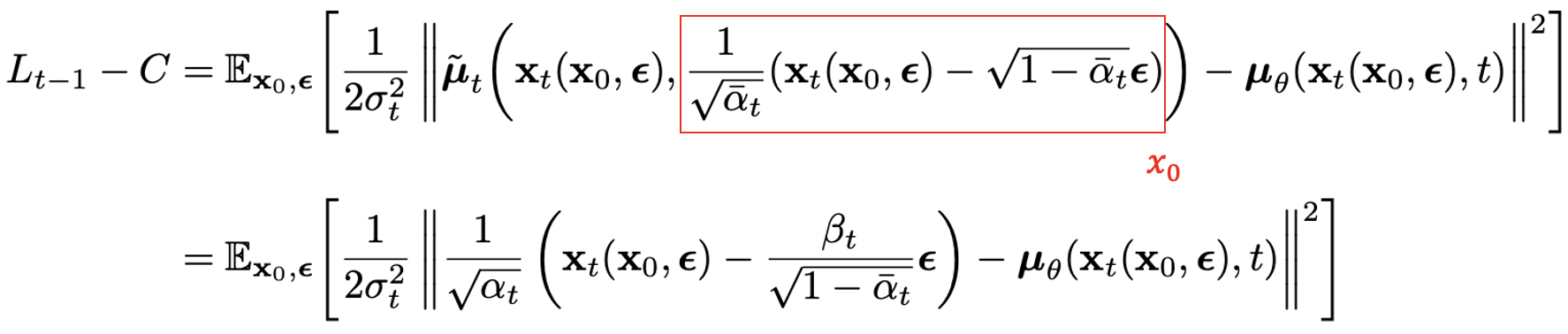
두 번째 식에 대한 증명은 생략하겠습니다(궁금하시다면 참고하세요). 이제 $\mu_{\theta}$는 $x_{t}$가 주어졌을 때, $\frac{1}{\sqrt{\alpha_t}}(x_{t}(x_{0},\epsilon)-\frac{\beta_t}{\sqrt{1-\bar{\alpha_t}}}\epsilon)$를 예측해야 하겠네요. 여기서 우리는 $x_{t}$는 network의 입력 값으로 받아올 수 있음을 생각해봅시다. 즉, 우리가 $\theta$를 활용해 모델링할 부분은 mean 전체가 아니라 noise $\epsilon$에만 국한될 수 있는 겁니다. 이 사실을 통해 우리는 $\mu_\theta(x_t,t)$를 아래와 같이 재정의할 수 있습니다.

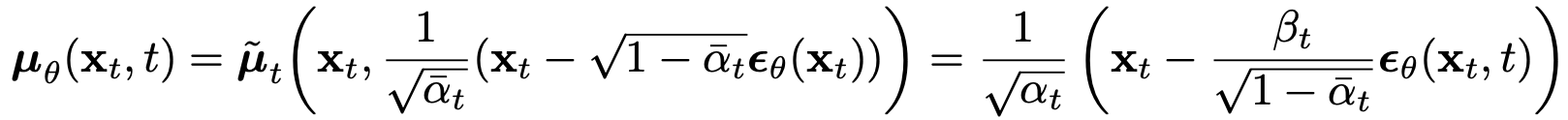
$\epsilon_{\theta}$는 $x_{t}$로 부터 $\epsilon$을 추측하는 network라 생각하시면 됩니다. 이제 $x_{t}$가 주어졌을 때, reverse process를 통해 $x_{t-1}$ 을 구하는 것은 $\frac{1}{\sqrt{\alpha_t}}(x_{t}(x_{0},\epsilon)-\frac{\beta_t}{\sqrt{1-\bar{\alpha_t}}}\epsilon_\theta(x_t,t))+\sigma_t\cdot z, \text{where} z\sim \mathcal{N}(0,I)$를 계산하는 것과 같아집니다. 이를 통해, 우리의 최종 loss 함수 $L_{t-1}$은 아래와 같이 noise에 관한 간단한 식으로 요약될 수 있습니다.

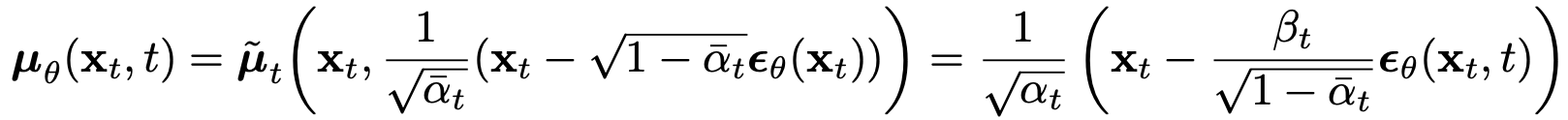
이 과정들을 요약하여 학습 과정으로 나타내면 아래의 Algorithm 1과 같이 나타낼 수 있습니다. 또한, Gaussian noise $x_{T}$로 부터 이미지를 복원해가는 inference 과정은 Algorithm 2처럼 나타낼 수 있습니다.

Conclusion

수식이 몹시 많고 복잡해보이긴 했지만, 생각보다 디테일을 조금씩 무시하면 큰 아이디어들은 직관적이고 따라갈만 했습니다. $L_{t-1}$을 denoising 관점으로 접근하여 학습하기 아주 용이한 형태로 만든 것이 DDPM의 핵심으로 느껴집니다. 조만간 stable diffusion, 혹은 3D 기반 생성 모델에 대한 포스팅으로 돌아오겠습니다. 감사합니다.