[Paper Review] Understanding Variational AutoEncoder

Diffusion 기반 생성 모델이 최근 크게 주목 받고 있다. Diffusion 모델을 공부하다 보면 피해갈 수 없는 게 바로 Variational AutoEncoder (VAE) 모델이다. Diffusion 모델을 제대로 이해하기 위해 최근 뒤늦게나마 VAE를 공부했다. 이번 포스팅을 통해 VAE의 아이디어와 학습 방법 등을 최대한 수식을 배제하고 간단하게 설명해보려 한다.

VAE의 목적

여느 생성 모델과 마찬가지로 VAE 또한 실제 데이터와 유사한 데이터를 생성하는 것을 목표로 합니다. 이를 위한 가장 간단하게는 아래와 같은 구조를 생각해볼 수 있습니다.

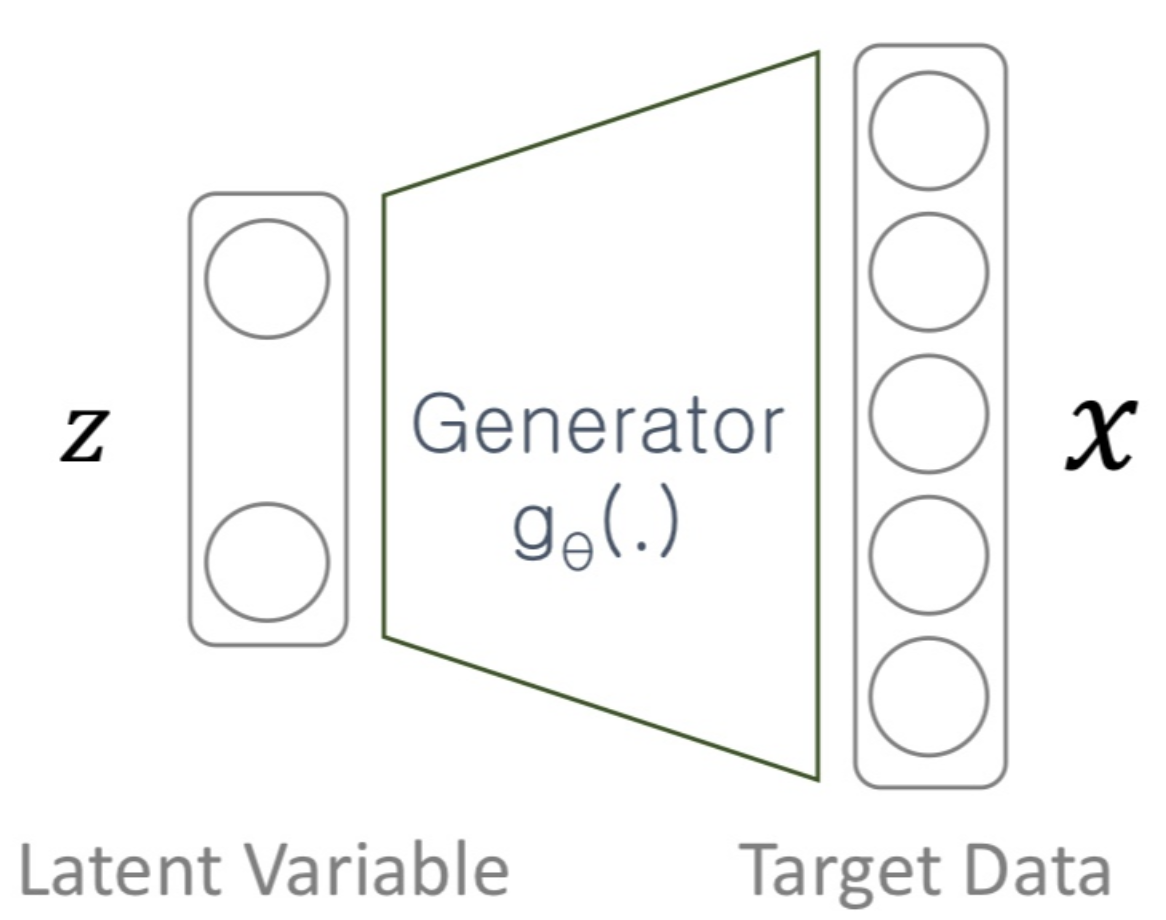
Latent $z$는 generator $g_{\theta}$를 거쳐서 생성 결과 $g_{\theta}(z)$를 만들어냅니다. 우리의 목적은 학습 데이터 속 $X$의 확률을 최대화하는 것이겠죠? 모든 $z$를 고려한 $X$의 확률은 아래와 같다.

$z$와 $\theta$가 주어지면 네트워크의 출력값은 deterministic한데, $P(X|z;\theta)$라는 개념은 어떻게 이해해야 될까요? VAE(뿐만 아니라 AutoEncoder 역시)의 출력 값이(실제와는 다르게) 아래와 같은 Gaussian 분포(Non-deterministic)를 따른다고 가정하곤 합니다.

풀어서 설명하면, $z$가 주어졌을 때 출력값 $X$의 확률 분포는 네트워크의 출력 값 $g_{\theta}(z)$을 평균으로 하고, $\sigma^{2}*I$을 분산으로 가지는 Gaussian 분포를 따른다는 뜻이죠. 하지만 네트워크의 출력 값은 $g_{\theta}(z)$로 deterministic하게 정해지지 않는가? 라는 궁금증이 생기실 겁니다. 물론 그렇지만, 학습을 위해 이를 변형시켜 생각하자는 겁니다. VAE는 학습 초반에(아마 후반에도) 주어진 학습 sample과 완전히 똑같은 출력 값을 만들진 못합니다. 따라서 우리는 VAE가 gradient descent를 통해 $X$와 유사한 값을 만들어 가도록 적절한 loss를 디자인해줘야 할겁니다. 그러나 네트워크의 출력 값이 deterministic하다고 해서, $P(X|z;\theta)$의 확률 분포를 Dirac delta 함수로 가정하면 likelihood를 최대화하기 위한 gradient descent를 행할 수 없게 됩니다. 따라서 네트워크의 출력 값이 Gaussian 분포를 따른다고 가정하는 것이고, 이 때 likelihood는 Euclidean distance가 작을수록 높게 나타납니다. 물론 꼭 Gaussian 분포로 가정할 필요는 없습니다.

Latent Sampling 방식의 문제점

다시 $P(X)$를 봅시다. $z$를 $n$번 sampling하여 $P(X)$를 근사하면 $P(X)\approx\sum_{i}P(X|g_{\theta}(z_{i}))p(z_{i})\approx\frac{1}{n}\sum_{i}P(X|g_{\theta}(z_{i}))$ 로 나타낼 수 있겠죠? 앞서 언급했듯, 이 때 likelihood는 Euclidean distance에 반비례합니다. 사실 이렇게 되면 문제가 생기는데, 아래 그림을 봅시다.

(a)와 같은 학습 데이터를 활용하여 모델을 학습시켰다고 가정합시다. 이 때, 샘플 (b)는 (a)의 글자에서 일부 픽셀을 지워낸 형태고, 샘플 (c)는 (a)의 픽셀을 조금씩 이동시킨 형태입니다. 우리가 보기에는 (c)가 실제 데이터(숫자 2)에 가깝지만, (b)와 (a) 사이의 Euclidean distance가 (c)와 (a) 사이의 거리보다 훨씬 작습니다. 즉, (c)의 likelihood가 (b)에 비해 훨씬 높게 측정된다는 것입니다. 이는 당연히 바람직하지 않은 모델이겠죠? 이 문제는 $z$를 uniform하게 sampling하여 $\sum_{i}P(X|g_{\theta}(z_{i}))p(z_{i})\approx\frac{1}{n}\sum_{i}P(X|g_{\theta}(z_{i})$ 처럼 근사가 된 것이 원인입니다. 즉, 우리는 조금 더 똑똑하게 $z$를 sampling할 필요가 있습니다. 여기서 VAE의 아이디어가 출발합니다.

$X$를 보여줄테니 $X$와 유사한 sample을 만들 수 있는 확률분포 $p(z|X)$를 만들고, 여기에서 sampling을 하자.

즉, 기존처럼 완전히 독립적인 분포 $p(z)$에서부터 $z$를 sampling하는 것이 아닌, $X$에 따라 변하는 $z$의 분포에서 sampling하는 것이 VAE의 핵심이라 이해하시면 됩니다. 이러한 이상적인 sampling 함수를 만들기 위해 우리는 $X$로 부터 유래된 $z$를 구하기 위한, 아래와 같은 구조를 취하게 됩니다.

앞서 설명한 구조와 다른 점은 posterior, 즉 encoder $q_{\phi}$를 통해 $z$를 생성한다는 점입니다. 만들어 놓고 보니 AutoEncoder와 구조가 비슷하지 않나요? 즉, VAE는 sampling을 영리하게 하자는 아이디어에서 출발해서 어쩌다 보니 AutoEncoder와 비슷한 구조를 가지게 된 것이지, 근본적으로 그 출발점은 AutoEncoder와 굉장히 다릅니다. 또한, encoder는 각 $X$에 대해 deterministic한 $z$를 출력하는 것이 아닌 $z$의 분포 자체를 추정하는 것이 목표이기 때문에, encoder의 출력 값은 $z$의 분포를 설명할 수 있는 평균 $\mu$ 값과 공분산 $\Sigma$로 이루어집니다. 또한, 뒤에서 설명할 reparameterization trick을 위해서 특정 $z$가 아닌, 분포를 추정하는 것이 훨씬 유리하다는 것을 설명하겠습니다.

ELBO

VAE는 AutoEncoder와 어떻게 다르게 학습되는 것일까? 많은 생성 모델들처럼, VAE 역시 maximum likelihood, $\text{log}(p_{\theta}(x))$를 최대화하는 방향으로 접근합니다.

$\text{log}(p_{\theta}(x))$는 전개하면 아래와 같습니다.

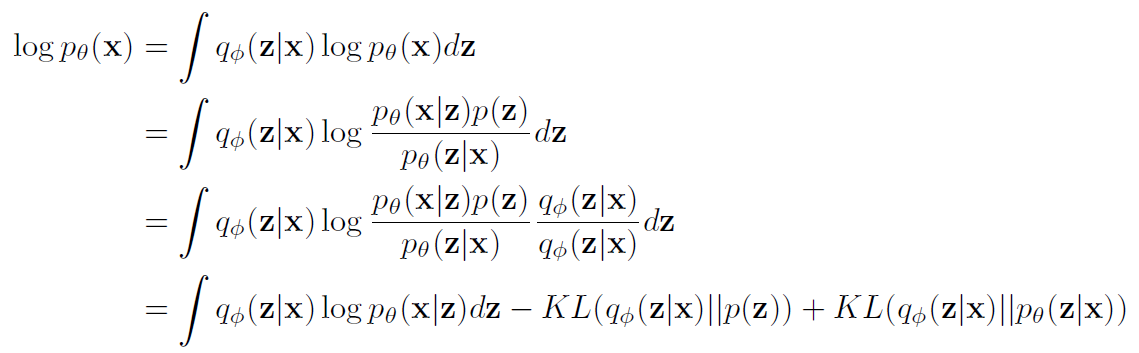
각각의 항을 살펴봅시다.

우선 첫 번째 항은 $x$가 입력으로 들어왔을 때, 나올 수 있는 $z$의 분포 $q_{\phi}(z|x)$에 대해서 $log p_{\theta}(x|z)$를 적분한 값입니다. 쉽게 설명하면, $x$가 encoder의 입력으로 들어왔을 때, decoder의 출력이 얼마나 $x$에 가까운지를 설명하는 항입니다. 그래서 이 부분을 reconstruction error라고 합니다.

두 번째 항의 경우 encoder를 통해 재정의된 $z$의 분포 $q_{\phi}(z|x)$와 원래 $z$의 분포 사이의 거리를 KL divergence로 표현한 값입니다. 두 번째 항의 경우, 새롭게 정의된 $z$의 분포인 posterior가 원래 $z$의 분포인 prior와 지나치게 많이 달라지는 것을 방지합니다. 그래서 이 부분을 regularization error라고 합니다.

마지막 항의 경우 우리가 알 수 없는 $p_{\theta}(z|x)$라는 값이 포함되어 있습니다. 그러나 우리는 KL divergence는 항상 양수라는 점을 활용하여, 아래와 같은 식을 유도할 수 있습니다.

$log p_{\theta}(x) \geq \text{Reconstruction Error} + \text{Regularization Error}$

이 때 reconstruction error와 regularization error의 합을 Evidence Lower BOund(ELBO)라 부르며, 이를 maximize함으로써 likelihood를 maximize합니다.

Reparameterization Trick

이제 ELBO를 계산해서 VAE를 학습시키면 되겠다! 라고 생각이 들지만, 저 식을 잘 생각해보면 계산하기 어려운 지점이 보일 겁니다. 바로 $q_{\phi}(z|x)$에 대한 적분을(첫 번째 항) 해야 합니다. 이를 위해서는 encoder의 출력으로 얻어진 분포 $\mathcal{N}(\mu, \Sigma)$에서 여러 번 sampling을 반복해서 연산을 해야 합니다. Forward 연산의 경우 이렇게 진행해도 (연산량은 많더라도) 문제는 없지만, backward의 경우 얘기가 달라집니다. Sampling은 미분 가능한 연산이 아니기 때문입니다. 따라서, reparametrization trick은 $z$의 분포를 미분이 가능하도록 바꿔주는 것이라 생각해도 무방합니다.

Reparameterization trick의 아이디어는 간단합니다. Stochasticity를 추가적인 noise $\epsilon \in \mathcal{N}(0,I)$로 옮겨주자. 즉, 우리가 연산해야 하는 $\mu$와 $\Sigma$에 대해서는 더 이상 stochasticity가 존재하지 않도록 아래와 같이 $z$를 재정의해봅시다.

이제 우리의 $z$는 $(\mu, \Sigma)$에 대해서 미분이 가능한 형태가 되었습니다. 이를 통해 우리는 이제야 마음 편하게 ELBO를 활용해 모델을 학습할 수 있게 되었습니다.

Conclusion

이미 stable diffusion까지 등장한 마당에 VAE의 생성 결과를 보여주는 건 큰 의미 없다고 생각해서 생략하겠습니다. VAE는 참 설명하기가 어렵군요. 꾸준히 포스팅을 할지는 모르겠지만, 다음 번엔 DDPM을 설명하는 글으로 돌아오겠습니다.