[Paper Review] GRAM: Generative Manifolds for 3D-Aware Image Generation

한참 diffusion 논문을 읽다가 본업으로 돌아와 다시 3D generator 관련 논문을 읽었습니다. 이번에 다룰 논문은 CVPR 2022에 Oral presentation으로 발표된 GRAM이라는 논문입니다. 사실은 GRAM 자체가 궁금했기 보단 GRAM을 활용한 다른 모델을 이해하기 위해서 읽었는데, 생각보다 재미있는 포인트들이 많아서 포스팅으로 남기게 되었습니다.

본 포스팅은 NeRF 모델에 대한 기본적인 이해가 있다는 가정 하에 작성되었습니다.

NeRF Sampling의 문제점

NeRF는 ray의 trajectory 위에서 균일하게 구간을 나누고, 각 구간에서 임의의 점을 sampling하는 Monte Carlo Sampling 방식을 취합니다. 그리고 각 지점에서 volume density를 계산한 후, density 분포를 토대로 hierarchical sampling(NeRF-H)를 재차 진행합니다. Density가 높은 부분이 최종 RGB에 영향을 줄 확률이 높으므로, density가 높은 부분에서 많은 횟수 sampling이 되도록 하는 똑똑한 전략인거죠. 이를 그림(출처)으로 표현하면 아래와 같습니다.

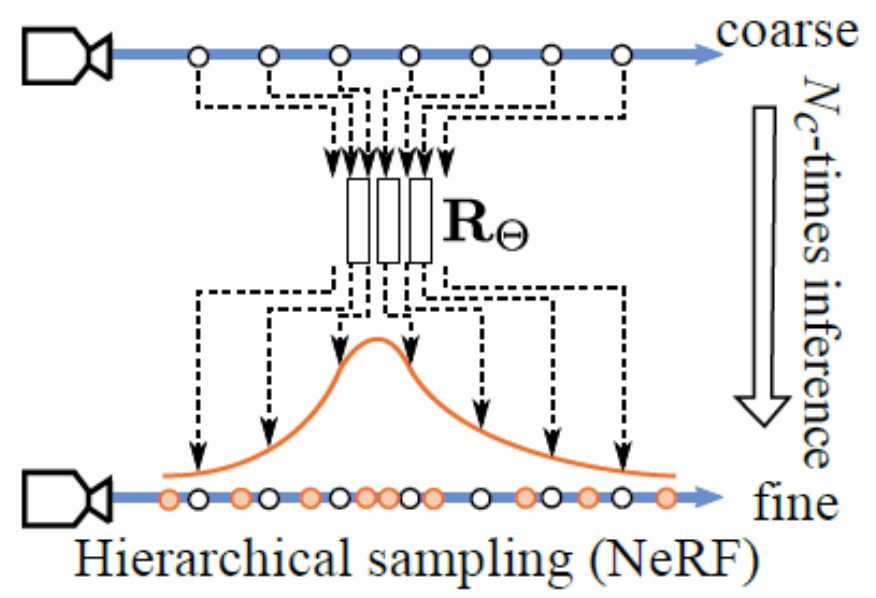
하지만 GRAM의 저자들은 이러한 sampling 방식이 문제가 된다고 주장합니다. 우선, Monte Carlo 기반의 Sampling을 사용하면 sample의 수가 적어졌을 때 생성되는 이미지의 품질이 굉장히 unstable 해진다고 합니다. 또한, sampling되는 point가 ray trajectory 위 interval에서 random하게 결정되다보니 이웃하는 ray임에도 sampling되는 point들 사이의 거리가 벌어질 수 있습니다. 그 결과, (이웃한 pixel임에도) integrate된 RGB 값도 크게 달라지게 되고, 이는 아래와 같이 원치 않는 noise pattern의 원인이 된다고 합니다.

저자들은 manifold prediction이라는 새로운 발상으로 이러한 문제를 돌파합니다.

Manifold Prediction

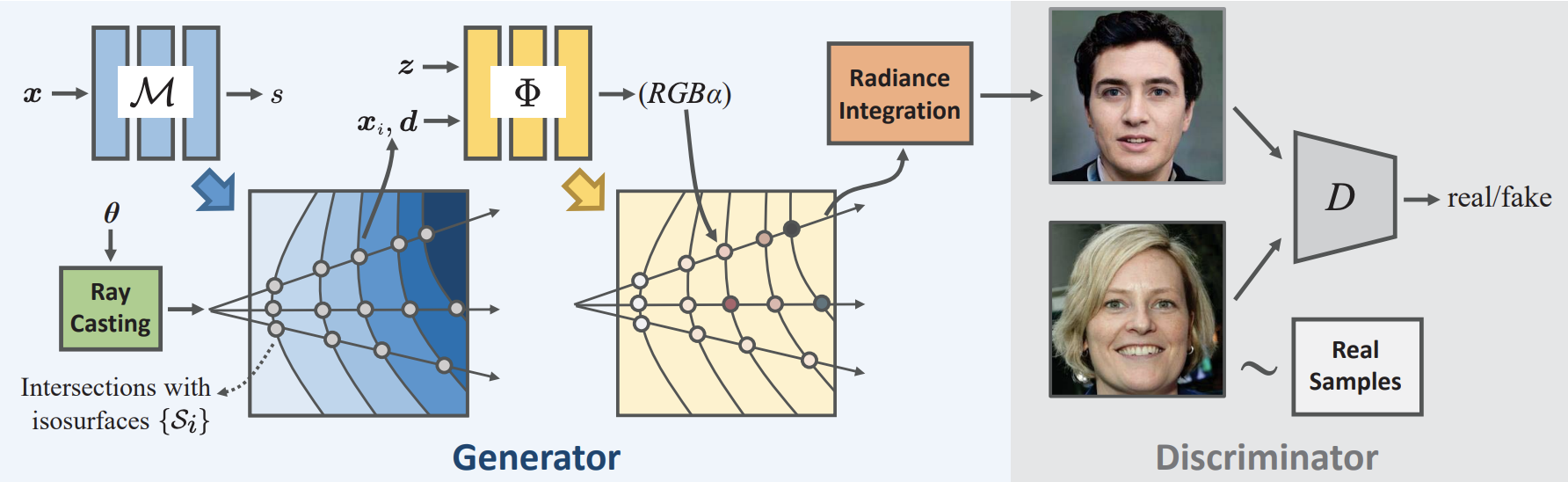
위 그림의 GRAM의 구조를 보면 이거저거 많이 들어가있긴 하지만, 사실 GRAM의 접근법은 너무나 단순해서(동시에 효과적입니다) 설명드릴 게 많지는 않습니다. 기존의 3D 기반 GAN과 가장 크게 다른 점은 바로 Manifold Predictor $\mathcal{M}$을 도입했다는 점입니다. $\mathcal{M}$은 아래와 같이 점의 좌표를 입력으로 받아 scalar 값 $s$를 예측하는 scalar field를 정의합니다.

여기서 우리는 각각 level ${l_i}$를 가지는 $N$개의 isosurface(직역하면 등위면 정도가 되네요)의 집합 $\lbrace S_i\rbrace =$ $\lbrace x|\mathcal{M}(x)=l_{i}\rbrace$를 정의해줍니다. 이 때, $l_i$는 학습을 통해 얻는 값이 아니라 미리 정의된 상수를 활용한다고 합니다. 이 scalar field 자체는 별 의미가 없기 때문에, 이 level 자체의 값이 중요하지는 않기에 임의로 설정해도 상관 없을 듯 합니다.

그렇다면 이 scalar field로 우리는 무엇을 할까요? 저자들은 여기서 굉장히 재미있는 제안을 합니다. Ray 위의 점들 중에서 isosurface와 교차하는 점만을 활용해서 rendering 하자 라고 말입니다. 수식으로 나타내면, 아래의 집합 ${x_{i}}$에 속하는 point를 지칭하는 것입니다.

여기서 $o$와 $d$는 ray의 원점과 방향, $t_n$과 $t_f$는 near plane과 far plane을 나타내는 parameter입니다. 다시 말하지만, radiance generator $\Phi$에는 이 집합에 속한 점들만 통과시키는 겁니다. 이 점들을 미분 가능한 연산 과정을 통해 구하는 과정이 논문에는 설명되어 있는데, 여기서는 생략하도록 하겠습니다. 아무튼 이렇게 얻어진 점의 좌표와 view direction $d\in\mathbb{R}^d$, 그리고 latent code $z$를 함께 radiance generation $\Phi$에 넣어 RGB color 값과 동시에 occupancy $\alpha$를 얻을 수 있다고 합니다. (저자들은 NeRF의 volume density 대신 occupancy를 활용한 rendering 방법을 채택했다고 하는데, 정확한 이유는 모르겠습니다.)

Training and Experimental Results

학습은 manifold predictor를 포함하여 모든 요소들이 joint하게 진행됩니다. Adversarial loss와 더불어 R1 regularization를 활용하여 아래와 같이 전체 학습 loss를 구성합니다.

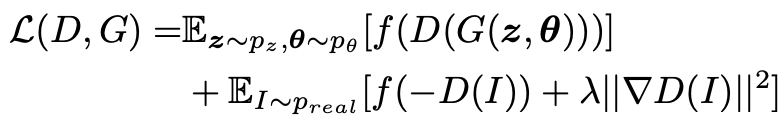
여기서 $p_{z}$와 $p_\theta$는 각각 latent code와 camera pose의 prior 분포이고, $f(u)=\text{log}(1+e^u)$로 정의되는 Softplus 함수입니다.

학습 결과는 아래와 같습니다.

학습된 manifold를 visualize하면 왼쪽 그림과 같아집니다. 개인적인 생각으로는 형상화하려는 mesh의 dilation을 취한 형태를 닮아 보입니다. 각각의 manifold 위에서 rendering되는 점들을 manifold 별로 visualize하면 오른쪽 그림과 같아진다고 합니다. Manifold 별로 뚜렷한 disentanglement가 보이지는 않는 거 같습니다.

저는 다른 실험 결과들보다도 ablation study 부분의 결과가 꽤나 흥미로웠습니다. 첫 번째 ablation study는 manifold 학습에 대한 부분입니다. NeRF-H를 baseline으로 비교했을 때, manifold를 학습하지 않고 spherical (학습 전 initialize 상태) 또는 plane처럼 단순한 형태로만 가정하더라도 성능이 눈에 띄게 좋아지게 됩니다.

또한, manifold learning을 적용하면 ray 당 sampling 개수를 크게 줄여도 FID가 크게 증가하지 않는 점도 신기했습니다. 아래 표에서처럼 Sampling point를 6개로, 통상적으로 쓰이는 64개 혹은 96개 보다 훨씬 적게 가져가면 NeRF-H의 경우 FID가 117로 굉장히 높게 나타나는 반면, GRAM의 경우 상대적으로 FID가 굉장히 작은 폭으로 증가하게 됩니다.

이 외에도 더 다양한 실험 결과를 확인하실 수 있습니다.

Conclusion

최근 NeRF의 성능이 점점 산업적 측면으로 쓰일 가능성이 보일만큼 발전했지만, 여전히 느린 inference time이 문제점으로 거론됩니다. Instant-NGP 등 NeRF inference 자체를 경량화하려는 노력도 많이 있지만 sampling point 수를 줄이는 것 역시 NeRF inference 가속에 큰 도움이 될 듯 합니다. 개인적으로 explicit parameter deformation을 활용하고 싶은데, 이 자체가 NeRF inference 만큼이나 time-consuming합니다. 그래서 sampling point 수를 줄이는, 아주 직관적인 방법으로 inference 경량화하는 데에 조금 더 관심이 갑니다. 때문에 저에게는 GRAM의 ablation study 결과가 꽤나 흥미로웠습니다. 기회가 된다면 GRAM을 제가 만들고 있는 모델에도 적용해봐야겠습니다. 감사합니다.