[Paper Review] 3D Gaussian Splatting for Real-Time Radiance Field Rendering

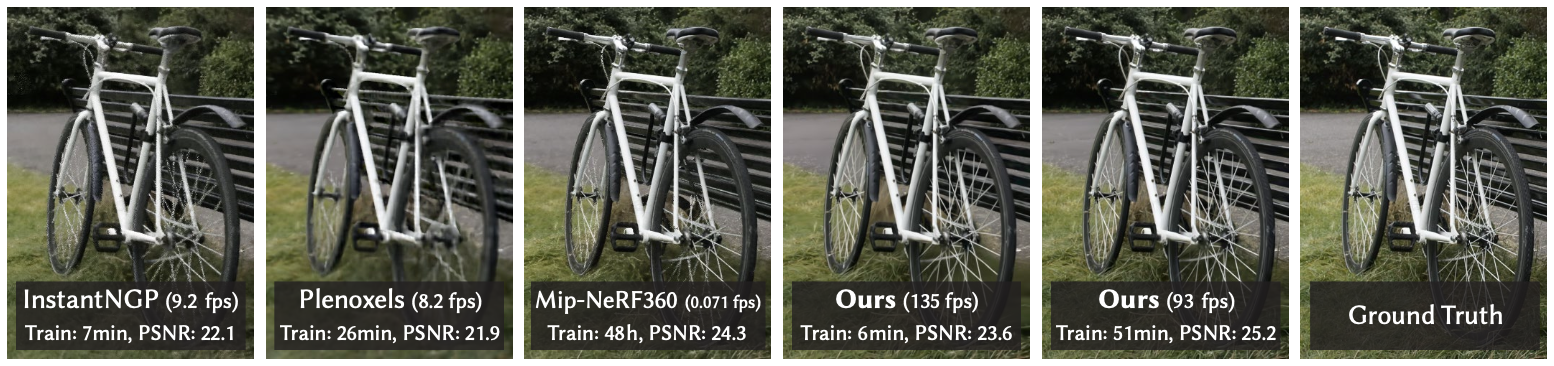
이번 ICCV2023에서 발표된 Gaussian Splatting 논문이 큰 화제입니다. 기존의 instant-NGP보다 훨씬 빠른 속도를 보여줌과 동시에, NeRF 기반 모델 중 가장 좋은 성능을 보이던 Mip-NeRF보다 좋은 rendering 성능을 보이기 때문입니다. 오늘은 Gaussian Splatting이 무엇이고, 어떤 방식으로 학습 및 렌더링을 진행하는지 간략하게 알아보려 합니다.

Gaussian Splatting

Gaussian Splatting의 구조는 아래와 같습니다. 각 요소에 대해서 보다 자세하게 알아봅시다.

Initialization

Gaussian Splatting Network는 아래 요소들을 입력으로 받습니다.

Image : 다양한 각도에서 촬영된 이미지들을 입력으로 받습니다. Gaussian Splatting은 static scene을 가정하기 때문에 이 이미지들은 동시에 촬영되었거나 멈춰있는 물체를 촬영했다고 생각하시면 됩니다.

Structure-from-Motion Output : Structure-from-Motion(SfM) 알고리즘은 이미지 별로 camera parameter, 그리고 point cloud를 반환합니다. 이 point cloud는 개략적인 물체의 구조를 나타낸다 생각해주시면 됩니다. 이 개념은 Nerfies를 비롯한 여러 NeRF 모델의 initialization에서도 활용되곤 했습니다. SfM이 익숙하지 않다면, 아래 Nerfies preprocessing 과정 중에 얻어진 point cloud와 camera visualization 그림을 참고해 주세요.

파랑색 점이 point cloud, 빨강색 점이 camera trajectory를 나타낸다고 생각하시면 됩니다. 아무튼 이렇게 얻어진 camera 정보와 point cloud는 Gaussian Splatting Network의 입력 값으로 활용됩니다.

이렇게 얻어진 point cloud들의 각 point는 각각 initial Gaussian 분포의 mean이 됩니다.

* Gaussian 분포로 volume을 표현하는 이유
1. Differentiable하게 volume의 분포를 표현할 수 있으며,
2. Mean과 variance만을 활용하여 explicit하게 표현 가능하며 (NeRF는 MLP를 통해 표현하는 implicit)
3. 효율적인 rasterization과 alpha-blending이 가능하기 때문입니다.

3차원에서의 Gaussian 분포는 아래와 같이 나타낼 수 있습니다 (상수계수 제외).

이러한 3차원 Gaussian은 여기의 과정을 거쳐 2D Gaussian으로 projection되어 rendering 가능하다 합니다. 이 과정은 본 포스팅에서는 아래 rasterization 설명하며 간단하게만 짚고 넘어가겠습니다. 그렇다면 $G(x)$를 학습하기 위해서는, 가장 직관적으로는 $\mu$와 $\Sigma$를 학습시키면 될 거 같습니다. 그러나 공분산 $\Sigma$는 positive semi-definite해야만 실제 volume을 가질 수 있습니다. 그러나 $\Sigma$ 내의 모든 parameter를 optimize한다면 positive semi-definite라는 성질이 유지될 것이라 장담할 수 없습니다. 그래서 저자들은 $\Sigma$를 직접적으로 optimize하기 보다 $\Sigma$를 표현하는 Scale과 Rotation matrix를 활용합니다.

아래 2차원 Gaussian의 visualization(출처)를 보면 타원으로 나타나는 것을 볼 수 있습니다.

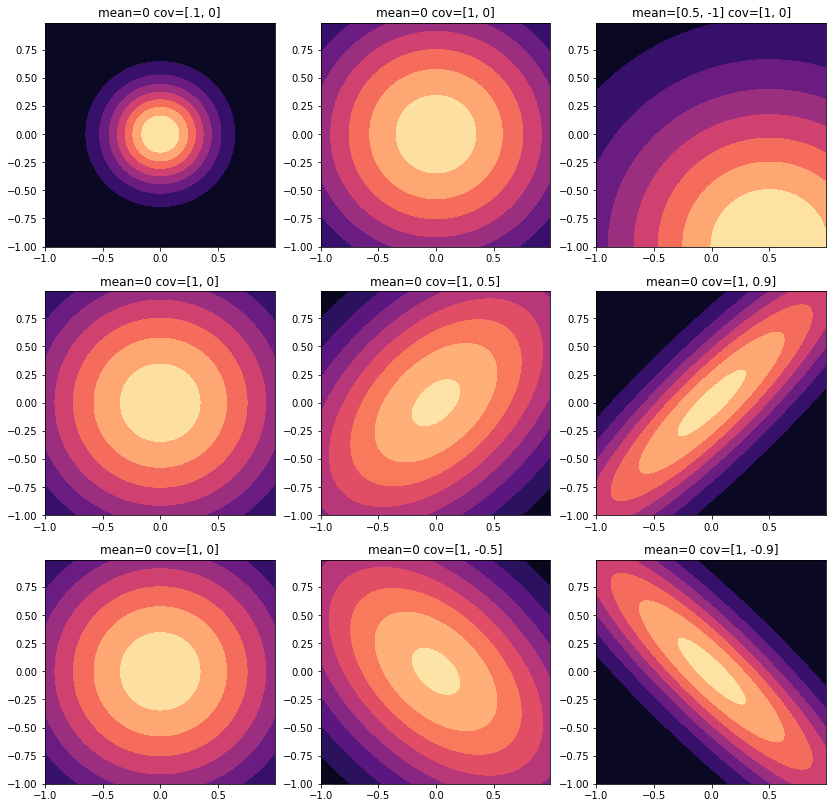
이 때, 타원의 중심은 mean이 결정하고, 타원의 scale과 rotation은 공분산이 결정하는 것을 볼 수 있습니다. 이는 3차원의 공간에서도 마찬가지입니다.

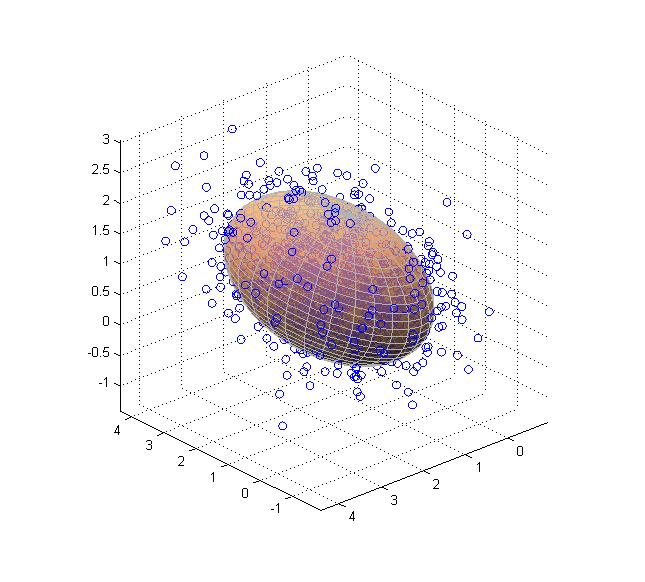
따라서, 위와 같은 타원형의 uncertainty ellipsoid의 모양을 결정하는 scale matrix와 rotation matrix를 활용하여 $\Sigma$를 나타낼 수 있습니다 (참고 : A geometric interpretation of the covariance matrix).

이 때, scale matrix와 rotation matrix만을 가지고 optimize를 한다면 $\Sigma$가 positive semi-definite을 유지하도록 할 수 있습니다. 정확히는 scale matrix와 rotation matrix를 구성하는 scale vector $s\in\mathbb{R}^{3\times 1}$ 와 quaternion vector $q\in\mathbb{R}^{4\times 1}$를 optimize한다고 합니다. 뭔가 의미적으로도 real volume을 나타내는 Gaussian을 학습시키는 것이라 그런지 $\Sigma$를 통째로 optimize하는 거보다 $s$와 $q$를 optimize하는 것이 자연스럽게 와닿기도 하네요.

Optimization

Initialization이 끝난 후, optimization을 진행해야 하는 변수들은 아래와 같습니다.

- position
- opacity
- covariance, 정확히는 scale vector 와 quaternion vector
- sphere-harmonic function coefficient

이 때, sphere-harmonic function은 Gaussian에게 비등방성(anisotropy)을 제공하기 위해 주어지는 함수입니다. 관측되는 방향에 따라서 color 값을 다르게 return하도록 하기 위한 장치라고 생각하시면 됩니다. NeRF에서는 비등방성을 구현하기 위해서 MLP의 입력으로 view direction을 coordinates와 함께 활용합니다. 손실 함수의 구성 자체는 NeRF와 유사합니다. Mean, $\Sigma$, color $c$, $\alpha$, camera pose $V$를 입력으로 받아서 rasterize(방법은 뒤에서 설명합니다)한 결과 $I$를 입력 이미지 $\hat{I}$와 비교하는 것입니다. 손실 함수는 $L_{1}$과 $L_{D-SSIM}$으로 이루어집니다.

Adaptive Control of Gaussians

그러나 위에서 설명한 optimization만을 활용해서는 Gaussian 분포의 개수를 바꿀 수는 없습니다. 그러나 처음 SfM을 통해 얻어진 점의 경우 sparse하고, 또 모든 volume을 표현하기에 부적합한 위치에 지정되었을 수도 있기에 이를 조정하는 과정이 필요합니다. 논문에서 Adaptive Control이라 지칭하는 과정은 아래 3가지 방법을 통해 분포의 개수를 조정합니다.

Remove : Hyperparameter인 $\epsilon_{\alpha}=0.005$보다 낮은 opacity를 가진 분포를 제거하는 과정입니다. 논문 내의 pseudo 알고리즘을 보면 Gaussian의 공분산이 너무 커서 observe하는 공간 전체를 포함하는 경우에도 큰 의미를 지니지 못하기 때문에 remove한다고 나와 있습니다.

위에 Remove가 존재하는 Gaussian을 줄여나가는 과정이라면, 이제부터 진행할 두 과정은 모두 Gaussian을 늘려나가는 과정입니다. 이 논문에서는 새로운 Gaussian을 무지성(?)으로 생성하기보단, 기존에 존재하는 Gaussian에서 clone 또는 split(두 방법론을 합쳐서 densify라고 부르겠습니다)하는 방법론을 제시합니다. 이 때, reconstruction을 잘 하고 있지 못하는 Gaussian을 densify하는 것이 효율적일 것입니다. 이를 판단하는 기준이 바로 view-space position gradient입니다. 제대로 reconstruct되고 있지 않는 position $p$에서의 gradient $\nabla_{p}L$ 값은 크게 나타날테니, 이를 densify 여부의 척도로 삼자는 것이 아이디어입니다. 존재하는 Gaussian 분포들 각각에서 position들을 sample하고, 이들 각각에서 $\nabla_{p}L$를 계산합니다. 만약 어떤 Gaussian에서 sample된 $p$들에서의 평균 $\nabla_{p}L$가 $\tau_{pos}$를 넘는다면, 이 Gaussian 주변은 제대로 reconstruct되고 있지 못하다고 해석할 수 있습니다. 이 경우, 해당 Gaussian을 densify를 하는 것입니다.

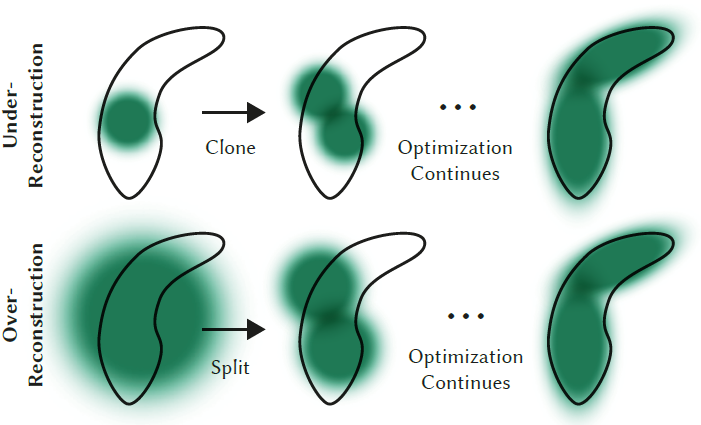
Densify를 하는 Gaussian은 크게 두 경우입니다. Gaussian이 geometric feature를 잘 재현하지 못하는 경우 (under-reconstruction), 또는 하나의 Gaussian이 너무 넓은 범위를 커버하고 있는 경우 (over-reconstruction)입니다. 각각의 경우는 위 그림을 보시면 더 이해가 잘 되실 겁니다. 각각의 경우, 어떤 방법으로 해결할 수 있는 지 알아봅시다.

Clone : Under-reconstruction의 경우에서 쓰이는 방법입니다. Positional gradient의 방향에 같은 크기의 Gaussian을 하나 더 복사(clone)한다고 생각하시면 됩니다. Positional gradient는 가장 reconstruct가 안되는 방향으로 향하고 있을테니, 여기에 Gaussian을 추가한다는 것은 reasonable한 방법인듯 합니다. 이 경우, Gaussian의 개수와 여기에 포함되는 전체 volume은 당연하게도 증가합니다.

Split : Over-reconstruction의 경우에서 쓰이는 방법입니다. 원래의 큰 Gaussian을 $\phi=1.6$ scale 만큼 줄어든 두 개의 Gaussian으로 나누어줍니다. 이 때, 각 Gaussian의 위치, 즉 mean 값은 원래의 큰 Gaussian의 PDF에서 sampling하여 얻어냅니다. 이 경우, Gaussian의 개수는 증가하지만 전체 volume은 거의 유사하게 유지하게 됩니다.

이런 식으로 optimization을 진행하면 다른 volumetric representation들과 마찬가지로 camera 근처의 floater들로 인해 Gaussian의 개수가 무작위로 증가하고, optimization이 진행되지 않을 수 있습니다 (floater에 대해서 정확히 이해하진 못했습니다). 이를 방지하기 위해 3000번의 iteration마다 $\alpha$ 값을 0으로 초기화 해주는 전략을 활용합니다. 이렇게 하면 Remove 단계를 통해서 필요 없는 Gaussian들을 주기적으로 지워줄 수 있습니다. 또한, 이를 통해서 Gaussian들이 중첩되는 현상 역시 줄여줄 수 있습니다.

Differentiable Tile Rasterizer

위처럼 얻어진 Gaussian들을 어떻게 2D image로 rasterize 시키는 지에 관한 알고리즘입니다. 논문만 봐서는 이해하기가 난해해서, 블로그 글을 많이 참고해서 작성했습니다. 아래의 pseudo 알고리즘을 보면서 단계 별로 설명 드리도록 하겠습니다.

CullGaussian

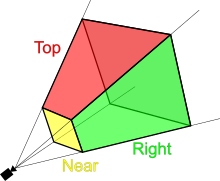
주어진 camera view에서 관측 가능한 Gaussian만을 선택하는 과정입니다. 아래와 같이 view frustrum 내에서 99%의 confident를 가지는 Gaussian만을 선택한다고 합니다. 또한, 저자들은 guard band라는 개념을 도입하여 extreme position에 위치한 Gaussian, e.g., mean이 near plane에 근접해 있거나 view frustrum 밖에 존재하는 경우, 들을 자동적으로 삭제한다고 합니다. 그 이유는 이러한 Gaussian들의 projection된 2D covariance를 계산하는 것이 unstable할 수 있기 때문이라고 합니다.

ScreenspaceGaussians

3D Gaussian을 rasterize하여 2D, 즉 Screen space로 projection하는 함수입니다. Viewing transform W가 주어졌을 때, cameara coordinates에서의 covariance $\Sigma^{‘}$은 다음과 같이 나타내어 집니다.

이 때, J는 projective transformation의 Jacobian입니다. 이 때, $\Sigma^{‘}$의 thrid row와 column을 skip하면, 같은 property를 가지고 있는 $2\times2$ covariance matrix를 얻을 수 있음을 증명한 논문이 있습니다. 이를 활용하여 3D Gaussian을 2D Gaussian으로 projection이 가능하다고 합니다.

CreateTiles

이미지를 $16\times16$, 총 256개의 tile로 쪼개줍니다.

DuplicateWithKeys

각 Gaussian을 overlap되는 tile의 개수만큼 instance화 시킵니다. 각 instance들은 view space depth와 tile ID를 조합하여 생성된 key를 할당받게 됩니다. 논문의 appendix를 참조하면 총 64bit의 사이즈로 이루어져 있으며, lower 32bit는 depth 정보를, higher 32bit는 tile ID 정보를 담고 있는다고 합니다.

SortByKeys

그 다음, 이 key들을 바탕으로 GPU Radix sort를 활용하여 Gaussian들을 sorting합니다. 각 tile마다 sorting은 병렬적으로 진행되며, 이를 통해 각 tile에 대해서 depth ordering한 결과를 얻을 수 있습니다. 이를 통해 더이상 pixel 별로 sorting을 활용하지 않아도 되기에 기존의 방법보다 훨씬 효율적이라고 이야기합니다.

IdentifyTileRanges

각 tile 별로 depth-sorted entry에서 첫번째와 마지막 entry를 identify하여 list를 만듭니다. 정확히는 무슨 과정인지 설명되어 있진 않습니다.

GetTileRange

이 연산은 모든 tile에 대해서 각각 수행됩니다. 모든 타일에 대해서 IdentifyTileRanges에서 구한 range R을 읽어옵니다.

BlendInOrder

Tile마다 pixel에 대해서 view depth가 작은 순부터 큰 순으로 color와 opacity 값을 accumulate합니다. 이 과정은 기존의 NeRF와 유사하다고 생각하셔도 됩니다. Gaussian Splatting에서는 tile마다 개별 CUDA thread block을 할당하여 병렬적 처리를 통해 연산 속도를 최소화하였다고 합니다.

Experimental Results

다양한 SOTA NeRF들과 비교한 결과입니다. Mip-NeRF와 거의 유사한 (30K의 경우 더 좋은 성능) 성능을 보이면서 동시에 Mip-NeRF보다 1,000배 이상 빠른 속도를 보이고 있습니다. Instant-NGP에 비해서도 대략 몇 십배 빠른 속도를 보여주고 있습니다. 기존의 NeRF처럼 point별로 많은 sampling을 진행하고, 이를 integrate하는 과정이 필요없다 보니, tile rasterizer의 속도가 기존 NeRF 기반 모델들보다 훨씬 좋은 성능을 보인다 생각합니다. 보다 많은 실험 결과는 논문을 참고하시길 바랍니다.

Conclusion

NeRF가 등장한지 불과 3년 정도 밖에 되지 않았는데 벌써 이를 대체할 만한 모델이 등장했다는 것에 놀랐습니다. Human avatar generation이 main interest인 저로서는 어서 dynamic scene에서 Gaussian Splatting이 얼마나 잘 동작할지 궁금합니다. 이미 몇몇 논문들이 Gaussian Splatting을 활용한 deformation 방법을 제시하고 있고, 이미 한 두개의 논문은 이를 활용해서 human avatar generation까지 다루고 있는 거 같습니다. 어서 dynamic scene에서의 Gaussian Splatting 논문을 읽어보고, 또 정리하러 오겠습니다. 감사합니다.